Prva vježba: geometrijske deformacije slika
U računalnom vidu često trebamo modificirati slike različitim geometrijskim deformacijama kao što su uvećanje, rotiranje ili izrezivanje. Ova laboratorijska vježba razmatra unatražne deformacije koje se najčešće koriste u praksi. Označimo ulaznu sliku s \(I_s\), izlaznu sliku s \(I_d\), vektor cjelobrojnih pikselskih koordinata s \(\mathbf{q}\) te parametriziranu koordinatnu transformaciju s \(\mathbf{T}_p\). Tada unatražnu deformaciju slike možemo formulirati sljedećim izrazom:
\[I_d (\mathbf{q}) = I_s (\mathbf{T}_p(\mathbf{q})) \ .\]Kako slike tipično imaju dvije geometrijske osi, i domena i kodomena koordinatnih transformacija odgovarat će Euklidskoj ravnini: \(\mathbf{T}_p : \mathbb{R}^2 \rightarrow \mathbb{R}^2\). U praksi se koriste različite vrste geometrijskih transformacija, ali najčešće koristimo afine, projekcijske i radijalne transformacije. Afine i projekcijske transformacije čuvaju kolinearnost točaka, dok radijalne transformacije ne utječu na udaljenost od ishodišta koordinatnog sustava.
Afine transformacije
Označimo početni 2D vektor realnih koordinata s \(\mathbf{q}_s\), konačni 2D vektor realnih koordinata s \(\mathbf{q}_d\), linearno ravninsko preslikavanje s \(A\),
te 2D pomak s \(b\). Tada afinu transformaciju ravnine možemo prikazati sljedećom jednadžbom:
Tablica prikazuje hijerarhijski popis vrsta afinih transformacija tako da svaka sljedeća vrsta odgovara poopćenju prethodne (\(\mathbf{I}\)=\(\mathrm{diag}(1,1)\), \(\mathbf{R}\) je matrica rotacije 2D podataka):
| transformacija | stupnjevi slobode | invarijante | ograničenja |
|---|---|---|---|
| translacija | 2 | orijentacija | \(\mathbf{A}=\mathbf{I}\) |
| transformacija krutog tijela | 3 | udaljenost | \(\mathbf{A}=\mathbf{R}\), \(\mathbf{R}^\top\mathbf{R}=\mathbf{I}\) |
| sličnost | 4 | kutovi | \(\mathbf{A}=s\mathbf{R}\), \(\mathbf{R}^\top\mathbf{R}=\mathbf{I}\) |
| općenita afina transformacija | 6 | paralelnost | nema |
Ako se odnos između dvije slike može opisati afinom deformacijom, onda parametre koordinatne transformacije možemo izlučiti iz korespondencija. Neka su u izvorišnoj slici \(I_s\) zadane točke \(\mathbf{q}\)si. Neka su u odredišnoj slici \(I_d\) zadane korespondentne točke \(\mathbf{q}_{di}\). Tada za svaki par korespondencija vrijedi:
\[\eqalign{ q_{si1} &= a_{11} q_{di1} + a_{12} q_{di2} + b_1\\ q_{si2} &= a_{21} q_{di1} + a_{22} q_{di2} + b_2}\]Ove dvije jednadžbe možemo presložiti tako da 6 parametara afine transformacije istaknemo kao nepoznanice te ih zapisati u matričnom obliku kako slijedi:
\[\left\lbrack \matrix{q_{si1} \cr q_{si2}} \right\rbrack = \left\lbrack \matrix{q_{di1} & q_{di2} & 0 & 0 & 1 & 0\cr 0 & 0 & q_{di1} & q_{di2} & 0 & 1} \right\rbrack \cdot \left\lbrack \matrix{a_{11} \cr a_{12} \cr a_{21} \cr a_{22} \cr b_{1} \cr b_{2}} \right\rbrack\]Ako dodamo još dvije korespondencije, dobit ćemo sustav \(6\times 6\) koji ima jedinstveno rješenje, osim ako su korespondencije kolinearne. Tražena deformacija biti će određena rješenjem tog sustava.
Projekcijske transformacije
Projekcijske transformacije ravnine možemo prikazati sljedećom jednadžbom:
\[\mathbf{q}_s = \mathbf{T}_p(\mathbf{q}_d) = \frac{\mathbf{A} \cdot \mathbf{q}_d + \mathbf{b}} {\mathbf{w}^\top\mathbf{q}_d + w_0} \ .\]Primijetite da je brojnik jednadžbe - vektor a nazivnik - skalar. Matrica \(\mathbf{A}\), vektori \(\mathbf{b}\) i \(\mathbf{w}\) te skalar \(w_0\) su parametri projekcijske transformacije. Parametre projekcijske transformacije možemo odrediti iz korespondencija na vrlo sličan način kao i za afine transformacije. Međutim, u ovom slučaju svaka korespondencija doprinosi dva homogena linearna ograničenja nad parametrima transformacije, do kojih dolazimo prebacivanjem nazivnika na lijevu stranu jednadžbe. To možemo napraviti kad god su korespondencije konačne jer je tada nazivnik sigurno različit od nule. Ako prikupimo \(n\) korespondencija, dobit ćemo homogeni linearni sustav s \(2n\) jednadžbi i devet nepoznanica oblika \(\mathbf{M}\mathbf{x}=\mathbf{0}\). Za vježbu raspišite koeficijente linearnog sustava za jednu korespondenciju!
S obzirom na to da su naše jednadžbe homogene, parametre projekcijske parametre možemo odrediti samo do proizvoljne multiplikativne konstante \(\lambda\neq 0\). Odatle zaključujemo da projekcijska transformacija ima samo osam stupnjeva slobode. Stoga ne čudi da će sustav \(\mathbf{M}\) imati točno jedno netrivijalno rješenje i ako prikupimo samo četiri korespondencije, pod pretpostavkom da niti jedna trojka korespondencija nije kolinearna. Rješenje sustava odgovara desnom singularnom vektoru matrice \(\mathbf{M}\) koji odgovara singularnoj vrijednosti nula. Ako imamo višak ograničenja (više od 4 korespondencije) optimalno rješenje u algebarskom smislu dobivamo kao desni singuarni vektor koji odgovara najmanjoj singularnoj vrijednosti matrice \(\mathbf{M}\).
Napominjemo da ovom problemu možemo pristupiti i ako odaberemo projekcijski prikaz korespondencija. U tom slučaju pokazalo bi se da projekcijsko preslikavanje možemo izraziti linearnom transformacijom homogenih koordinata točaka projekcijske ravnine. Projekcijski prikaz doveo bi do tri jednadžbe po svakoj korespondenciji, a dvije od tih triju jednadžbi bile bi jednake kao i gore. To nije veliki nedostatak jer bismo i inače mogli koristiti samo dvije jednadžbe jer treća jednadžba odgovara linearnoj kombinaciji prve dvije. Jedna prednost projekcijskog pristupa jest mogućnost jednostavnog uklapanja s korespondencijama u beskonačnosti (nedogledima), ali to nam nije presudno jer ovdje pretpostavljamo da su sve korespondencije unutar slike.
Interpolacija slike u realnim koordinatama
Ranije smo najavili da unatražnu deformaciju slike formuliramo sljedećim izrazom:
\[I_d (\mathbf{q}) = I_s (\mathbf{T}_p(\mathbf{q})) \ .\]Primijetimo da koordinatna transformacija nije diskretna, tj. da 2D vektor \(\mathbf{T}_p(\mathbf{q})\) ima realne koordinate. To znači da u odredišni piksel \(\mathbf{q}\) valja upisati element izvorne slike koji se nalazi “između” njenih piksela. Aproksimativno uzorkovanje diskretnih slika u realnim koordinatama nazivamo interpolacijom. Postoji više interpolacijskih pristupa, a ovdje ćemo upoznati interpolaciju najbližim susjedom i bilinearnu interpolaciju.
Interpolacija najbližim susjedom
Interpolacija najbližim susjedom naprosto preuzima vrijednost najbližeg piksela. Koordinate najbližeg piksela dobivamo zaokruživanjem realnih koordinata na najbliže cjelobrojne vrijednosti:
\[I(r+\Delta r, c+\Delta c)_{NN} = I(\lfloor r+\Delta r+0.5 \rfloor, \lfloor c+\Delta c+0.5 \rfloor )\]Bilinearna interpolacija
Bilinearna interpolacija pretpostavlja da elementi slike na realnim koordinatama linearno ovise o udaljenosti od poznatih diskretnih piksela. Slika pokazuje da interpolirani slikovni element dobivamo kao linearnu kombinaciju susjedna četiri piksela, pri čemu veću težinu dobivaju pikseli koji su bliži realnim koordinatama. Tako interpolirani element dobivamo kao plava površina puta I(r,c) plus zelena površina puta I(r,c+1) plus narančasta površina puta I(r+1,c) plus crvena površina puta I(r+1,c+1).
Prikazani odnosi matematički se mogu prikazati sljedećom jednadžbom: \(I_{BL}(r+\Delta r, c+\Delta c) = I(r,c) \cdot (1-\Delta r)(1-\Delta c) + I(r,c+1) \cdot (1-\Delta r)\Delta c + I(r+1,c) \cdot \Delta r(1-\Delta c) + I(r+1,c+1) \cdot \Delta r\Delta c\)
Napominjemo da bi se ista jednadžba dobila i kad bismo zrcalili vertikalnu koordinatu odnosno kad bi indeksi redaka rasli prema gore. Za usporedbu, interpolacija najbližim susjedom bila bi jednaka donjem lijevom pikselu jer je on najbliži zadanim realnim koordinatama. Takvo stanje stvari odražava i činjenica da je narančasti pravokutnik veći i od plavog i od zelenog i od crvenog pravokutnika.
Detaljniji prikaz bilinearne interpolacije kao i recept za učinkovitu implementaciju mogu se pronaći u završnom radu Petre Bosilj.
Zadatak 1: interpoliranje
Napišite kod koji učitava sliku, te na nju primjenjuje slučajnu afinu transformaciju primjenom i) interpolacije najbližim susjedom te ii) bilinearnom interpolacijom. Upute:
- poslužite se slikama
scipy.misc.ascent()iscipy.misc.face() - matricu \(\mathbf{A}\) slučajne afine transformacije zadajte ovako:
A = .25*np.eye(2) + np.random.normal(size=(2, 2)) - vektor \(\mathbf{b}\) slučajne afine transformacije zadajte tako da se središnji piksel odredišne slike preslika u središnji piksel izvorišne slike
- napišite funkciju
affine_nn(Is, A,b, Hd,Wd)koja izvorišnu slikuIsdeformira u skladu s parametrimaAibte odredišnu sliku rezolucijeHd\(\times\)Wdvraća u povratnoj vrijednosti; odredišni pikseli koji padaju izvan izvorišne slike trebaju biti crni; funkcija treba koristiti interpolaciju najbližim susjedom te funkcionirati i za sive slike i za slike u boji - napišite funkciju
affine_bilin(Is, A,b, Hd,Wd)koja radi isto što iaffine_nn, ali s bilinearnom interpolacijom - neka odredišna rezolucija bude
Hd\(\times\)Wd= 200\(\times\)200 - karakterizirajte odstupanje odgovarajućih piksela dobivenih s
affine_biliniaffine_nn(uputa: ispišite korijen srednjeg kvadratnog odstupanja piksela dvaju slika) - neka vaš glavni program odgovara sljedećem kodu:
import matplotlib.pyplot as plt
import scipy.misc as misc
import numpy as np
Is = misc.face()
Is = np.asarray(Is)
Hd,Wd = 200,200
A,b = recover_affine_diamond(Is.shape[0],Is.shape[1], Hd,Wd)
Id1 = affine_nn(Is, A,b, Hd,Wd)
Id2 = affine_bilin(Is, A,b, Hd, Wd)
# dodati ispis standardne devijacije
fig = plt.figure()
if len(Is.shape)==2: plt.gray()
for i,im in enumerate([Is, Id1, Id2]):
fig.add_subplot(1,3, i+1)
plt.imshow(im.astype(int))
plt.show()
Zadatak 2: procjena afine transformacije iz korespondencija
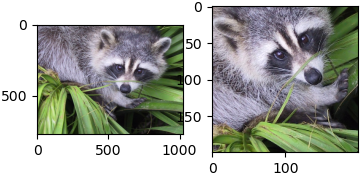
Napišite funkciju recover_affine_diamond(Hs,Ws, Hd,Wd) koja vraća parametre afine transformacije koja piksele središta stranica izvorišne slike dimenzija Hs\(\times\)Ws preslikava u kuteve odredišne slike dimenzija Hd\(\times\)Wd. Istestirajte vaše parametre provođenjem deformacije iz prve vježbe.
Upute:
- za rješavanje sustava jednadžbi koristite
np.linalg.solve - slika prikazuje ulaz i izlaz deformacijskog potprograma ako za izvorišnu sliku odaberemo
misc.face()
Zadatak 3: procjena projekcijske transformacije iz korespondencija
Napišite funkciju recover_projective(Qs, Qd) koja vraća parametre projekcijske transformacije ako su zadane točke izvorišne slike Qs i točke odredišne slike Qd. Upute:
- za rješavanje homogenog sustava koristite
np.linalg.svd - odredišne točke postavite na kuteve odredišne slike
- prikažite rezultate obrade za više slučajno odabranih točaka izvorišne slike
